能力综合提升-字符串-1
0x01 字符串哈希
字符串哈希通过牺牲很小的准确率,达到快速进行字符串匹配的效果。
就单向加密嘛,很简单。可以多次哈希减小出错概率。
1.1 P3370【模板】字符串哈希
题意:对字符串数组去重,求出剩余字符串的个数。
当然可以用 std::map,但我们要练习哈希的写法。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
vector<ull> v;
ull Hash(string &s)
{
ull res = 0;
for(auto i : s)
res = res * 37 + i * i;
// 这里我认为就是随机乱搞,搞出什么都差不多,利用的是 ull(18446744073709600000) 的自然溢出,大概率不会出问题
return res;
}
signed main()
{
int n; cin >> n;
F(i, 1, n)
{
string s; cin >> s;
v.push_back(Hash(s));
}
sort(v.begin(), v.end());
cout << unique(v.begin(), v.end()) - v.begin();
return 0;
}
1.2 P5270 无论怎样神树大人都会删库跑路
题意:给定一个长为 $T$ 的 $S$ 串,$n$ 个小字符串 $a_i$,长为 $m$ 的数组 $R$,初始一个空字符串 $X$。进行 $Q$ 次操作,每次操作会把小字符串 $a_{(i - 1) \bmod m + 1}$ 放到 $X$ 的末尾。每次操作如能存在一个后缀使得任意排列后能变成 $S$,ans ++;。求 ans。注意 $S$ 串的元素是 $[1, 10^5]$ 的数字而非字符。
本题关键:任意排列后能变成 $S$,本质上是两个字符串比较是否相等的问题,可以用字符串哈希。因为每个位置字符的地位是平等的,因此 hash 函数应当是位置无关的。
先考虑 $Q \leq m$ 的情况。
只需要模拟字符串放入的过程,保留最后 $T$ 位,比较哈希值即可,使用前缀和维护。
注意,如果仅把 hash 函数设为 $f=\sum x$,冲突可能性极大。因此需要多个 hash 函数来避免哈希冲突。
我使用的 Hash 函数是:
1
2
3
4
5
6
int f1(int x) {return x;}
int f2(int x) {return x * x;}
int f3(int x) {return x * x + 5;}
int f4(int x) {return x * 3;}
int f5(int x) {return sqrt(x);}
int f6(int x) {return pow(x, 1.55);}
再考虑,如果 $Q > m$,则 $Q$ 可分解为 $Q = k * m + d$。
对于 $m$ 不是太小的情况,可以计算出以下三部分:
- 在循环节内部匹配的个数 $ans_1$
- 在循环节之间匹配的个数 $ans_2$
- 最后剩余 $d$ 个匹配的个数 $ans_3$
最终答案就是 $ans = ans_1 \times k + ans_2 \times (k - 1) + ans_3$。
代码是真的很难写。
为了防止难写的代码写好多次,我的做法是,重复两次循环节,到 $m$ 时记录 $ans_1$,到 $m + d$ 时记录 $ans_3$,到 $2m$ 时记录 $ans_2$。但是这里又多出来了 $ans_1$ 的部分,要减掉,所以答案就是 $ans_1\times k + (ans_2 - ans_1) \times(k - 1) + ans_3$。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
int n, m, T, Q;
int R[maxn << 1];
int del[maxn << 1]; // 表示第 i 位已经被删掉了几个
vector<int> v[maxn << 1];
vector<int> S;
class HASH
{
private:
vector<int> val;
public:
HASH(){}
HASH(vector<int> &a, int (*f)(int)) // 函数指针表示 Hash 函数避免多写
{
val.resize(a.size() + 1);
F(i, 1, a.size())
val[i] = val[i - 1] + f(a[i - 1]);
}
int qry(int i)
{
return val[i];
}
~HASH(){}
};
// Hash 函数
int f1(int x) {return x;}
int f2(int x) {return x * x;}
int f3(int x) {return x * x + 5;}
int f4(int x) {return x * 3;}
int f5(int x) {return sqrt(x);}
int f6(int x) {return pow(x, 1.55);}
// Hash 前缀和
HASH a[7][maxn << 1];
signed main()
{
read(n, T, Q);
// 特判 Hack 数据,真的不想调了呜哇
// Hack 数据的本质是 m 不够大时有横跨多个循环节的匹配出现
if(n == 9) {puts("2"); return 0;}
else if(n == 1) {puts("8"); return 0;}
// 读入
F(i, 1, T)
S.push_back(readint());
F(i, 1, n)
F(j, 1, readint())
v[i].push_back(readint());
F(i, 1, m = readint())
read(R[i]);
// 预处理 Hash 前缀和
F(i, 1, n)
{
a[1][i] = HASH(v[i], f1);
a[2][i] = HASH(v[i], f2);
a[3][i] = HASH(v[i], f3);
a[4][i] = HASH(v[i], f4);
a[5][i] = HASH(v[i], f5);
a[6][i] = HASH(v[i], f6);
}
a[1][0] = HASH(S, f1);
a[2][0] = HASH(S, f2);
a[3][0] = HASH(S, f3);
a[4][0] = HASH(S, f4);
a[5][0] = HASH(S, f5);
a[6][0] = HASH(S, f6);
if(Q <= m)
{
// 由下面的情况直接复制而来,看下面即可
}
else
{
// Q = k * m + d;
int k = Q / m, d = Q - k * m;
// 避免出现正好整除的情况使得不能统计 ans2
if(d == 0)
k --, d = m;
// 当前长度
int l = 0;
// 当前串的 Hash 维护
vector<int> b(7);
int ans1 = 0;
// 左右指针,左边是删除右边是插入
int pl = 0, pr = 0;
F(awa, 1, m)
{
pr ++;
// 加入该串
l += v[R[pr]].size();
F(i, 1, 6)
b[i] += a[i][R[pr]].qry(v[R[pr]].size());
// 还没满足就直接润
if(l < T)
continue;
// 一直删
while(l - T >= v[R[pl]].size() - del[pl])
{
// 注意 Hash 的部分扣除和 del 数组有关
F(i, 1, 6)
b[i] = b[i] + a[i][R[pl]].qry(del[pl]) - a[i][R[pl]].qry(v[R[pl]].size());
l -= v[R[pl]].size() - del[pl];
del[pl] = v[R[pl]].size();
// 指针右移
pl ++;
}
F(i, 1, 6)
b[i] = b[i] + a[i][R[pl]].qry(del[pl]) - a[i][R[pl]].qry(del[pl] + l - T);
del[pl] += l - T;
l = T;
// 比较 Hash 查询,统计答案
bool ans = true;
F(i, 1, 6)
ans = ans && (a[i][0].qry(S.size()) == b[i]);
ans1 += ans;
}
// 下面同理不讲
int ans2 = 0;
int ans3 = 0;
F(awa, 1, m)
{
R[awa + m] = R[awa];
pr ++;
l += v[R[pr]].size();
F(i, 1, 6)
b[i] += a[i][R[pr]].qry(v[R[pr]].size());
if(l < T)
continue;
while(l - T >= v[R[pl]].size() - del[pl])
{
F(i, 1, 6)
b[i] = b[i] + a[i][R[pl]].qry(del[pl]) - a[i][R[pl]].qry(v[R[pl]].size());
l -= v[R[pl]].size() - del[pl];
del[pl] = v[R[pl]].size();
pl ++;
}
F(i, 1, 6)
b[i] = b[i] + a[i][R[pl]].qry(del[pl]) - a[i][R[pl]].qry(del[pl] + l - T);
del[pl] += l - T;
l = T;
bool ans = true;
F(i, 1, 6)
ans = ans && (a[i][0].qry(S.size()) == b[i]);
ans2 += ans;
if(awa == d)
ans3 = ans2;
}
// 答案式子见推导
write('\n', ans1 * k + (ans2 - ans1) * (k - 1) + ans3);
}
return 0;
}
1.3 P5537 系统设计
题意:给定一个 $n$ 个点的有根树,长度为 $m$ 的序列 $a$,实现 $q$ 个操作,
操作分两种:
1 x l r表示设定起点为有根树的节点 $x$,接下来依次遍历 $l \sim r$。当遍历到 $i$ 时,从当前节点走向它的编号第 $a_i$ 小的儿子。如果某一时刻当前节点的儿子个数小于 $a_i$,或者已经遍历完 $l \sim r$,则在这个点停住,并输出这个点的编号,同时停止遍历。2 t k表示将序列中第 $t$ 个数 $a_t$ 修改为 $k$。
观察性质:
$a$ 序列会改变,但树的形态不会改变
给定的序列固定,其遍历的节点也随之固定
最终有效的(让遍历节点更改的)序列一定是 $l\sim r$ 的一个前缀。且最终答案的前缀序列的任意前缀一定合法,其余前缀不合法。也就是说具有单调性。
从 $u$ 出发到 $v$ 可以看作从根节点出发经过 $u$ 再到 $v$。
于是可以预处理出树上任意遍历前缀。接着用二分 $l\sim r$ 的前缀,并加上 $root\sim x$ 这段路径,看是否在之前的预处理中出现过。那么这个可以用 Hash 进行快速比较。
引用自 lupengheyyds 的 题解。
代码没写。
0x02 KMP
KMP 算法是模式串匹配的一种算法,能够将最坏 $O(nm)$ 的时间复杂度优化到 $O(n+m)$。
其中的 next 数组具有优美的性质,next[i] 表示字符串的前 $i$ 位的最长 border 的长度,border 定义为 $s$ 的一个真子串 $t$ 满足 $t$ 既是 $s$ 的前缀又是 $s$ 的后缀。
border 的性质:border 的 border(如果存在)还是 border。
2.1 P3375 【模板】KMP
题意:字符串匹配每个位置,并输出每个 next[i]。
代码熟练背诵。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
char a[maxm], b[maxm];
int nxt[maxm];
int main()
{
scanf("%s\n%s", a + 1, b + 1);
int al = strlen(a + 1), bl = strlen(b + 1);
for(int i = 2, j = 0; i <= bl; i ++)
{
while(j && b[i] != b[j + 1])
j = nxt[j];
if(b[i] == b[j + 1])
j ++;
nxt[i] = j;
}
for(int i = 1, j = 0; i <= al; i ++)
{
while(j && a[i] != b[j + 1])
j = nxt[j];
if(a[i] == b[j + 1])
j ++;
if(j == bl)
{
write('\n', i - bl + 1);
j = nxt[j];
}
}
F(i, 1, bl)
write(' ', nxt[i]);
return 0;
}
2.2 P4391 Radio Transmission 无线传输
题意:一个字符串 $s_2$ 自我复制若干次的子串为 $s_1$,给 $s_1$ 求 $s_2$ 的最短长度。
本题考查 KMP 的 next 数组的性质。
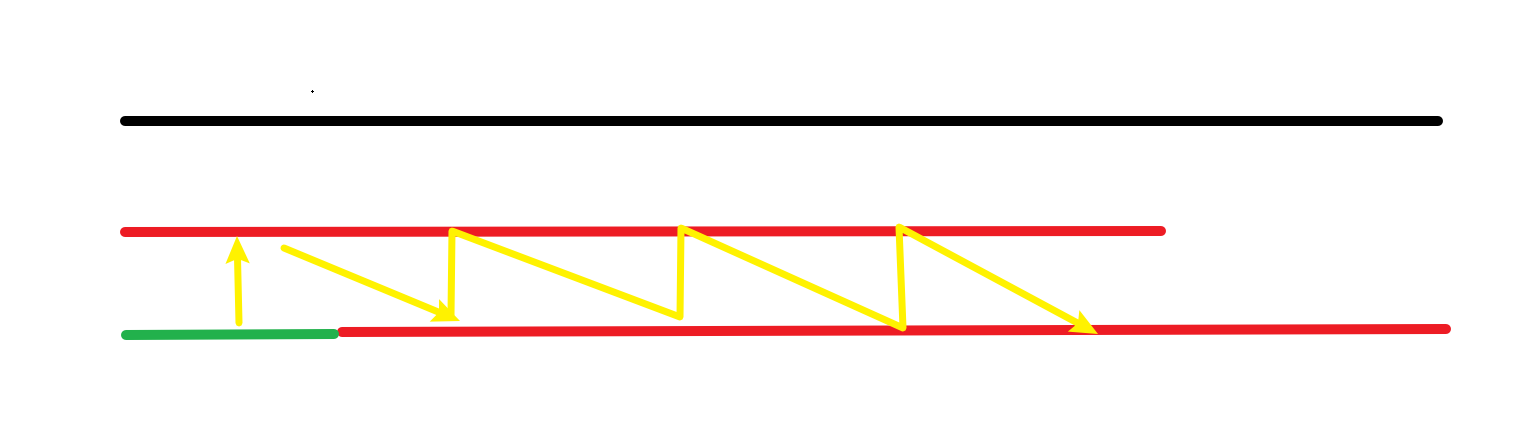
红色部分为最长的 border。观察绿色部分,由黄箭头所指,这两部分相同;又因为 border 是相同的前后缀,所以沿着黄色箭头这些部分都相等。这也就满足了题目中“自我复制”的要求。
最终答案就是 n - next[n]。
2.3 P3435 OKR-Periods of Words
题意:规定 $Q$ 是 $s$ 的周期当且仅当 $Q$ 是 $s$ 的真前缀且 $s$ 是 $Q+Q$ 的前缀。求给定字符串所有前缀的最大周期的和。
同样考察 next 数组的性质。因为 KMP 算法里最有意思的就是 next 数组,花样最多。
分析题意,周期的概念等价于一个真前缀复制后把非前缀部分的重合,也就是说这是一个 border。为了让周期最大,border 要最小才行。又由性质知 border 的 border 还是 border,也就是说可以重复跳 next 直到跳到空。
但是这样复杂度会出问题,如果给你 $10^6$ 个 a,每次跳 next 只会减少 $1$,复杂度是 $O(n^2)$ 的。此时我们可以借鉴并查集路径压缩的思想,暴力跳完之后直接将 next 修改为最小的 border,这就完成了路径压缩,时间复杂度为 $O(n)$。
要开 long long。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
int n;
char s[maxm];
int nxt[maxm];
signed main()
{
scanf("%lld\n%s", &n, s + 1);
for(int i = 2, j = 0; i <= n; i ++)
{
while(j && s[i] != s[j + 1])
j = nxt[j];
if(s[i] == s[j + 1])
j ++;
nxt[i] = j;
}
int ans = 0;
for(int i = 2, j = 2; i <= n; j = ++ i)
{
while(nxt[j])
j = nxt[j];
if(nxt[i])
nxt[i] = j;
ans += i - j;
}
write('\n', ans);
return 0;
}
2.4 P4824 Censoring S
题意:字符串匹配,匹配到就删除,输出最后结果。
要注意删除的时候,删除前后两段可能拼成目标串造成二次删除。
怎么做呢?考虑开一个栈,栈内存放着保留的下标;匹配完成之后就弹出匹配串的长度,同时 j 跳到 i - len 当时对应的 j 的位置(用数组记录),继续下次匹配。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
char s[maxm], t[maxm];
int nxt[maxm];
int stk[maxm], top;
int f[maxm];
signed main()
{
scanf("%s\n%s", s + 1, t + 1);
int sl = strlen(s + 1);
int tl = strlen(t + 1);
for(int i = 2, j = 0; i <= tl; i ++)
{
while(j && t[i] != t[j + 1])
j = nxt[j];
if(t[i] == t[j + 1])
j ++;
nxt[i] = j;
}
for(int i = 1, j = 0; i <= sl; i ++)
{
while(j && s[i] != t[j + 1])
j = nxt[j];
if(s[i] == t[j + 1])
j ++;
f[i] = j;
stk[++ top] = i;
if(j == tl)
{
top -= tl;
j = f[stk[top]];
}
}
F(i, 1, top)
putchar(s[stk[i]]);
return 0;
}
2.5 P2375 [NOI2014] 动物园
题意:定义 num[i] 为字符串前 $i$ 位的所有长度不大于 $\frac{i}{2}$ 的 border 的个数。求所有的 num[i]。
num[i] 自然可以通过不断跳 next 得到,但是这太不优秀了,考虑如何优化。
你考虑,假定我们拥有一个数组 f 记录所有的 border 个数(也就是 num 数组的弱化版),那当我们暴力跳 next 的时候一旦 $j\leq \frac{i}{2}$ 时,num[i] 就是 f[j] 了。
这个 f 可以在求 next 数组的时候递推求出,总复杂度是 $O(n)$ 的。
另外,注意到在使用 f[j] 的时候 num[j] 已经被使用过了,于是这两个数组可以合并,类似滚动数组。
插播唐诗笑话一则:我先赋初始值,然后把整个数组初始化了。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
char s[maxm];
int nxt[maxm];
int num[maxm];
void mian()
{
int ans = 1;
scanf("%s", s + 1);
n = strlen(s + 1);
memset(nxt, 0, sizeof(nxt));
memset(num, 0, sizeof(num));
num[1] = 1;
for(int i = 2, j = 0; i <= n; i ++)
{
while(j && s[i] != s[j + 1])
j = nxt[j];
if(s[i] == s[j + 1])
j ++;
nxt[i] = j;
num[i] = num[j] + 1;
}
for(int i = 2, j = 0; i <= n; i ++)
{
while(j && s[i] != s[j + 1])
j = nxt[j];
if(s[i] == s[j + 1])
j ++;
while(j > (i >> 1))
j = nxt[j];
ans = (ans * (num[j] + 1ll)) % mod;
}
write('\n', ans);
}
0x03 Manacher
Manacher 是一种求解回文子串的算法。
3.1 【模板】manacher
依然熟练背诵。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
constexpr int maxn = 1.1e7 + 10;
char s[maxn << 1];
int p[maxn << 1], cnt, ans;
void input()
{
char ch = getchar();
s[0] = '~'; s[cnt = 1] = '|';
while(!isalpha(ch)) ch = getchar();
while(isalpha(ch)) s[++ cnt] = ch, s[++ cnt] = '|', ch = getchar();
}
signed main()
{
input();
for(int i = 1, r = 0, mid = 0; i <= cnt; i ++)
{
if(i <= r)
p[i] = qmin(p[mid * 2 - i], r - i + 1);
while(s[i - p[i]] == s[i + p[i]])
p[i] ++;
if(p[i] + i > r)
r = p[i] + i - 1, mid = i;
eqmax(ans, p[i]);
}
write('\n', ans - 1);
return 0;
}
注意:做隔板字符的字符可以是任意的,因为只有可能真值和真值匹配,隔板和隔板匹配。
0x04 Trie
把字符上树。为 AC 自动机做铺垫。
4.1 阅读理解
题意:统计每个单词在哪几篇短文中出现过。
用作 Trie 板子题练习。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
int n, m, k;
struct Node
{
char val;
int nxt[26];
set<int> vis;
int findnxt(int x)
{
return nxt[x - 'a'];
}
void setnxt(int x, int v)
{
nxt[x - 'a'] = v;
}
Node(char v)
{
val = v;
memset(nxt, 0, sizeof(nxt));
}
};
vector<Node> Trie(1, Node(0));
void build(string &s, int idx)
{
int ptr = 0;
F(i, 0, s.length() - 1)
{
if(!Trie[ptr].findnxt(s[i]))
{
Trie.push_back(Node(s[i]));
Trie[ptr].setnxt(s[i], Trie.size() - 1);
}
ptr = Trie[ptr].findnxt(s[i]);
}
Trie[ptr].vis.insert(idx);
}
void query(string &s)
{
int ptr = 0;
F(i, 0, s.length() - 1)
{
if(!Trie[ptr].findnxt(s[i]))
{
cout << endl;
return;
}
ptr = Trie[ptr].findnxt(s[i]);
}
for(auto i : Trie[ptr].vis)
cout << i << " ";
cout << endl;
}
signed main()
{
ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
cin >> n;
F(i, 1, n)
{
cin >> m;
F(j, 1, m)
{
string s; cin >> s;
build(s, i);
}
}
cin >> n;
F(i, 1, n)
{
string s; cin >> s;
query(s);
}
return 0;
}