2025 ICPC 西安交通大学校赛 —— 20250518游记
0x00 赛前
提前两天 vp 了去年的校赛题目,感觉还不错啊!
自己唐了好多发,有心理阴影了。
最后分工定的是:ytc ABCD,awa EF+数学诈骗题,yth 速看可做题。
0x01 赛时
草台班子开始显现,这个这个网络登不上了,非常好笑。
注意到 B 题的题目名是 《全都登不上》,更好笑了。
赛时听说 B 的出题人就是维护网络出锅的人,笑不活了。
先看 E,咋放博弈论啊。考虑 $E\to 0$,$H\to 1$,$F=E\to 0$,然后猜了一个选择无关模拟即可的结论。我不敢确定正确性啊!先看下题。
F 是你妈交互???四次询问查 $x\in [1,5\times 10^9]$ 的整数,四次?但是看到只需要保证猜的数 $x^\prime$ 满足 $x \in[\frac{1}{2}x^\prime, 2x^\prime]$ 即可。一眼二分啊!但是在哪里分点呢?没有想法。
这个时候 yth 告诉我 L 是一道 awa 的题目。诶诶诶诶诶?你的意思是,我作为选手做到了以自己为背景的题目??
看眼 O,感觉没什么思路,过了。
这个 H 倒是很有魔方那味道,其实还真是。那么本质上就是先中心后棱块再角块。然后把模式暴力存入就行。
这个时候 ytc 写完 ABC,D 小唐一发,然后我上来写 E。他们首先对这个做法产生了质疑,随后用奇偶性严格证明了结论。比较谨慎的一发过了。
然后我立刻开始写 H。写的比较谨慎,同时验证了好多次。感觉完全不会超出 81 次的限制的样子。队友跟我说多测几组样例手玩一下。玩了半天气笑了,我代码不就是在模拟这个过程吗?那直接输出模拟结果不就可以检验了嘛。最后一发过了。
此时我们伟大的 yth 发出一声怪叫并且让我们验证一个东西是否是 Fibnacci 数列乘起来。这是啥注意力啊?
我去看 O 了。给定 $1\leq a, c, p\leq 10^9$,让你给出任意一个 $1\leq b\leq 10^{18}$ 满足 $a^b\equiv b^c\pmod p$。
显然的想法是离散对数,这题也是这样的,但是没思路啊。
试了试常见的 $a^c,c^a$ 啥的都不行。我灵机一动啊!考虑 Fermat 小定理,$a^{p-1}\equiv 1\pmod p$,那我就让 $b=p-1$ 试试?看右边,$b^c=(p-1)^c=(-1)^c$,那么在 $c$ 是偶数的时候就成立了!奇数的情况怎么办呢?
考虑 $(-1)\times(-1)=1$ 呢!也就是说,让 $b=(p-1)\times(p-1)$,左边是 $1^{p-1}=1$,右边是 $(-1)^{2c}=1$!也就是输出 $(p-1)\times(p-1)$ 即可,与 $a,c$ 都无关!一发过了。
然后 yth 仅用七分钟的时间写完了 M 题,拿下了首杀金气球。这道题被出题组认为仅次于防 AK 题的难度。我草,注意法秒了,牛逼兄弟。
得到了手刹的 AD 钙奶。我喝了两瓶。
下面开始写 F。因为据说前六题保证最简单嘛。ytc 一看就想出来,“对 $\log_2 x$ 进行二分不就行了”!这是正确的,因为 $x\in [\frac{1}{2}x^\prime,2x^\prime] \Longleftrightarrow \log_2 x\in[\log_2 x^\prime -1, \log_2 x^\prime +1]$!于是我立刻写了一个这样的东西。WA 了。
为什么?我们尝试测试 $1,5\times 10^9$,才发现一个致命问题:它不够稠密,导致有些东西被扔在外面,查不到。怎么办?
最后还是 ytc 先想到,我也很快想到,整数是离散的,因此我们可以分块更广一点。如果说 $2\in[1,4]$ 的话,下一个区间的中心就可以是 $10\in[5,20]$ 了。因为 $(4,5)$ 之间没有整数嘛。
这也让我们警觉这个 $n\leq 5\times 10^9$ 并非空穴来风。打表发现 $f_{16}=5.7\times 10^9$,刚好卡在边界上!也就是说如果是 $10^9$ 的话应该已经被第一种做法草完了。
呃,WA了。
yth:你他妈读入 $n$ 了吗?
Wrong Answer。
yth:你他妈保证每次询问 $x\leq n$ 了吗?
我操!这个 $n$ 原来是有用的啊!按理来说确实一点用不用吧!
Wrong Answer。
awa:你他妈保证最终回答 $x^\prime \leq n$ 了吗?
我操!这什么题!你妈的!整整吃了六发罚时,彻底不读题。红温了。
最后开 N 和 L。我们说的是 L 是数据结构题,用数据结构维护一个朴素转移 $O(n^2)$ 的 dp。然后 N 是一个 $\operatorname{mex}$ 题,我没做过这样的题目,因此我想不到某些很典的套路。
ytc 发现以 $\operatorname{mex}=1,2,\cdots,n$ 的区间构成了一个区间套,在这些区间里存在偏序关系 $\subset$,因此 可以对区间二分来确定该区间的 $\operatorname{mex}$。这个看起来很真啊!但是我没写这块代码,查错也吃了六发罚时。
L 彻底倒闭。我们用线段树维护了 $x_i+vt_i$ 和 $x_i-vt_i$。然后发现还有一个边界没法表示!我操,这不就是树套树吗!
但是时间不够了,为什么呢?
1
2
3
4
5
6
7
8
9
10
11
void update(int l, int r, int rt, int pos, int val)
{
if(l == r)
{
tr[rt] = val;
return ;
}
update(l, mid, ls, pos, val);
update(mid + 1, r, rs, pos, val);
tr[rt] = max(tr[ls], tr[rs]);
}
这能忍住不笑的都是神人了。关键是我真没看出来。因为真的太久没写线段树了。
最后还剩 7 min,没办法走人了。
结束的时候 ytc 说要搞个红绿灯。yth 死活不同意。那就不搞吧。
0x02 赛后
出题人对于秒了 M 很吃惊,询问我们做法。总之是一大堆精彩的讨论。
发现 L 可以转换一下,对一个排序另一个做最长不下降子序列就行了。妈妈生的。
吃不下去饭啊!直接去主 D-105 了。
讲题。
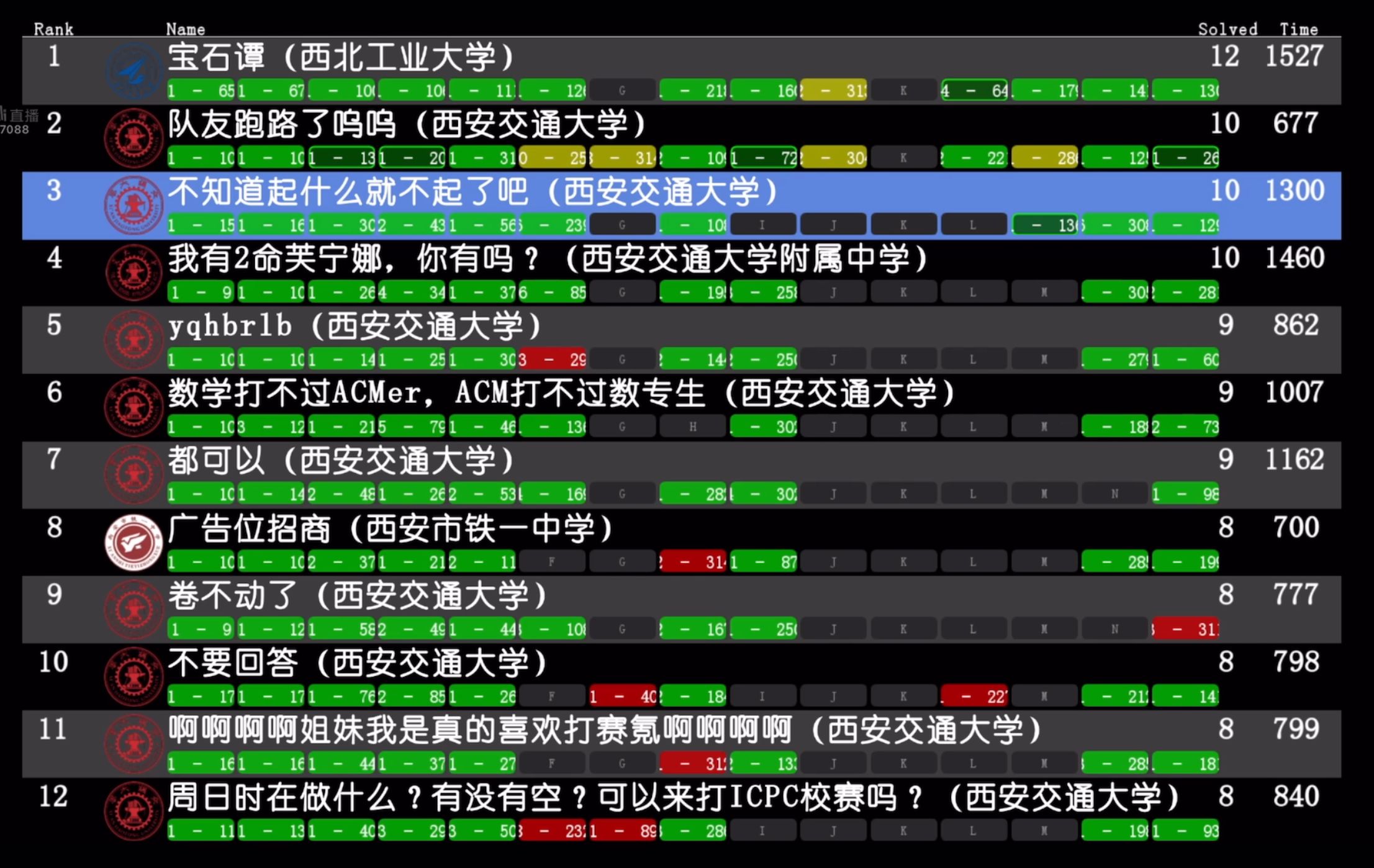
滚榜。
铜牌线和银牌线都是五题,笑死我了。什么区分度。
金牌线八题,还行。
不知道起什么就不起了吧。
最后被单挑的 E_Space 薄纱。
晚上还是出去吃了。